引论

编译器与解释器

编译器（C/C++）

  • 读入某种语言（源语言）编写的程序
  • 直接输出另一种语言（目标语言）编写的程序
  • 通常目标程序可执行

解释器（Python/Java）

  • 直接利用用户输入执行源程序中的操作
  • 不生成目标程序，而根据语义直接运行

编译器的结构

前端（分析部分）

前端部分是机器无关的。

  • 把源程序分解成组成要素、相应的语法结构
  • 依此结构创建源程序的中间表示
  • 收集源程序相关的信息，存放到符号表

后端（综合部分）

后端部分是机器有关的。

  • 根据中间表示和符号表信息构造目标程序

编译器工作步骤

字符流 -> 词法分析器 -> 符号流 -> 语法分析 -> 语法树 -> 语义分析 -> 语法树 -> 中间代码生成器 -> 中间表示形式 -> 机器无关代码优化器 -> 中间表示形式 -> 代码生成器 -> 目标机器语言 -> 机器相关代码优化器 -> 目标机器语言

符号表

词法分析

功能

  1. 读入字符流，组成词素，输出词法单元序列
  2. 过滤空白、换行、制表符、注释等
  3. 将词素添加到符号表中
  4. 在逻辑上独立于语法分析，但是通常和语法分析器处于同一趟中（词法分析器与语法分析器有交互）

词法单元(token)

<token-name, attribute-value>

  • token-name是表示词法单位种类的抽象符号，语法分析器通过token-name即可确定词法单元序列的结构
  • attribute-value通常用于语义分析之后的阶段

模式(pattern)

描述了一类token的lexeme可能具有的形式

词素(lexeme)

  • 源程序中的字符序列
  • 与某个token的模式匹配，被词法分析器识别为该词法单元的实例
printf("Total = %d\n", score);
token 非正式描述 lexeme example
if 字符i, f if
else 字符e, l, s, e else
comparison <, >, <=, >=, ==, != <=, !=
id 字母开头的词/数字串 Pi, score, var2
number 数字常量 3.14159, 0, 6.02e23
literal 在两”间的，除”外的任何字符 “This is a string.”

∴

printf, score => id

"Total = %d\n" => literal

token的规约

字母表(alphabet)：一个有穷的符号集合（用Σ表示）

  • 符号典型例子：字母、数字、标点符号

串(string)：字母表中符号的有穷序列

  • 空串：长度为0的串，ε

  • 前缀(prefix)：从串的尾部删除0个或多个符号后得到的串

    • banana => ban

  • 后缀(suffix)：从串的头部删除0个或多个符号后得到的串

    • banana => nana

  • 子串(substring)：删除串的某个前缀和某个后缀得到的串

    • banana => nan

  • 真前缀、真后缀、真子串：既不等于原串，也不等于空串的前缀、后缀、子串

  • 连接(concatenation)：

  • 指数运算：

语言(language)：某个给定字母表上的串的可数集合。

语言的运算

运算 定义和表示
L和M的并 L∪M={ s | s属于L或s属于M }
L和M的连接 LM={ st | s属于L且t属于M }
L的Kleene闭包 L* = Ui=0∞ Li
L的正闭包 L+ = Ui=1∞ Li

克林闭包（Kleene）可以出现空串ε，而正闭包长度至少为1。

运算优先级：

( a ) | ( ( b ) * ( c ) ) = a | b * c

正则集合：

以L(r)表示满足正则表达式（下文统称为regex）r 的集合。

Σ = { a , b }

L( a | b ) = { a , b }

L( (a | b) (a | b) ) = { aa , ab , ba , bb }

L( a* ) = { ε , a , aa , aaa , aaaa , … }

L( (a | b)* ) = { ε , a , b , aa , ab , ba , bb , aaa , aab , … }

L( a | a * b ) = { a , b , ab , aab , aaab , … }

若L(r) = L(s)，那么 regex r和s等价。

regex代数定律

定律 描述
r | s = s | r | 满足交换律
r | ( s | t ) = ( r | s) | t | 满足结合律
r ( st ) = ( rs ) t 连接运算满足结合律
r ( s | t ) = rs | rt; ( s | t ) r = sr | tr 连接对 | 可分配
εr = rε = r ε是连接的单位元
r* = ( r | ε )* 闭包中一定包含ε
r** = r* *具有幂等性

regex扩展运算符

operator equivalence
+ rr*
? ε | r
[a1a2…an] a1 | a2 | … | an
[a-e] a | b | c | d | e

其中+可表一个或多个实例，?可表零个或一个实例。

token的识别

定义ws → (blank | tab | newline)+来消除空白，当词法分析器识别出这个模式时，不返回词法单元， 继续识别其它模式。

以下是词法单元模式与regex对照表：

pattern regex
digit [0-9]
digits digit+
number digits(.digits)?(e[+-]?digits)?
letter [A-Za-z]
id letter(letter|digit)*
if if
then then
else else
relop < | > | <= | >= | = | <>(!=)

状态转换图

状态：表在识别lexeme时可能出现的情况。

  • 状态看作是已处理部分的总结
  • 若状态为接受状态或最终状态，表明已找到词素
  • 加上*的接受状态表示最后读入的符号不在词素中
  • 初始状态：用Start边表示

边：从状态指向另一状态。

  • 当前状态为s，下一个输入符号为a，就沿着从s离开，标号为a的边到达下一个状态

relop token的状态转换图：

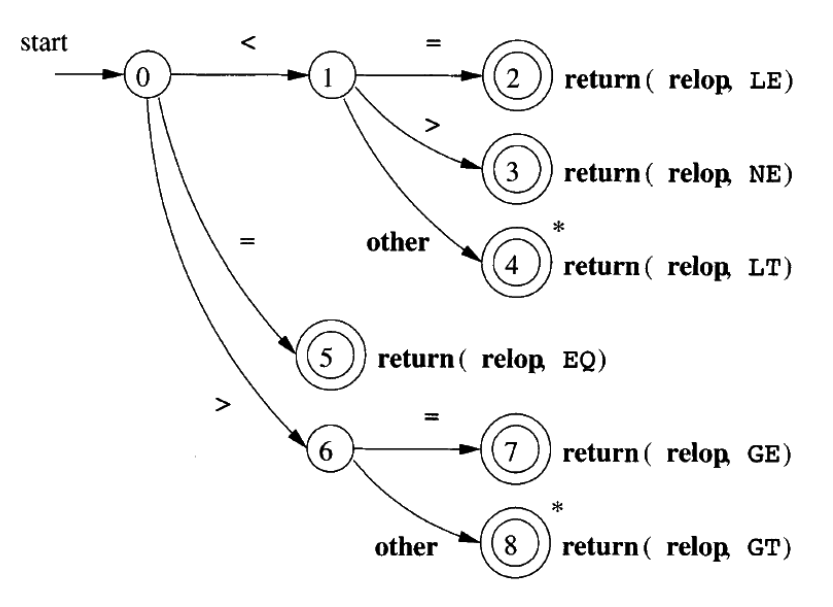
e1058abc38afd60a30f57cd3b427bbe5.png

return value full statement
NE not equal
LE less equal
LT less than
GE greater equal
GT greater than

从状态转换图到词法分析器

  • 维护变量state记录当前状态
  • 维护一个switch语句根据state跳转至相应代码段
    • 根据读入符号确定下一状态
    • 若找不到相应边，调用fail()进行错误恢复
  • 进入接受状态时，返回相应的token
    • 状态标有*时，需回退forward指针

以下是一种可能的实现方法

#include <iostream>

std::string code(">=");
int forward = 0;

enum class RelopAttribute {
    NE, LE, LT, GE, GT, EQ
};

struct TOKEN {
    RelopAttribute attribute;
};

void fail() {
    //implementation...
}

char getNextChar() {
    return code[forward++];
}

void retract() {
    --forward;
}

void printAttribute(const TOKEN& token) {
    std::string attr;
    switch (token.attribute) {
        case RelopAttribute::NE:
            attr = "NE";
            break;
        case RelopAttribute::LE:
            attr = "LE";
            break;
        case RelopAttribute::LT:
            attr = "LT";
            break;
        case RelopAttribute::GE:
            attr = "GE";
            break;
        case RelopAttribute::GT:
            attr = "GT";
            break;
        case RelopAttribute::EQ:
            attr = "EQ";
            break;
        default:
            break;
    }
    std::cout << attr;
}

TOKEN getRelop() {
    TOKEN res;
    int state = 0;
    while (true) {
        char c = getNextChar();
        switch (state) {
            case 0:
                if (c == '<') {
                    state = 1;
                } else if (c == '=') {
                    state = 5;
                } else if (c == '>') {
                    state = 6;
                } else {
                    fail();
                }
                break;
            case 1:
                if (c == '=') {
                    state = 2;
                } else if (c == '>') {
                    state = 3;
                } else {
                    state = 4;
                }
                break;
            case 2:
                res.attribute = RelopAttribute::LE;
                return res;
            case 3:
                res.attribute = RelopAttribute::NE;
                return res;
            case 4:
                retract();
                res.attribute = RelopAttribute::LT;
                return res;
            case 5:
                res.attribute = RelopAttribute::EQ;
                return res;
            case 6:
                if (c == '=') {
                    state = 7;
                } else {
                    state = 8;
                }
                break;
            case 7:
                res.attribute = RelopAttribute::GE;
                return res;
            case 8:
                retract();
                res.attribute = RelopAttribute::GT;
                return res;
            default:
                fail();
        }
    }
}

int main() {
    TOKEN token = getRelop();
    printAttribute(token);
    return 0;
}
C:\Users\17253\CLionProjects\CompilerDesign\cmake-build-debug\CompilerDesign.exe
GE
进程已结束，退出代码为 0

保留字的识别

我们需要在符号表中预先填好保留字，并指明它们不是普通的标识符。

为保留字建立的独立的、高优先级的状态转换图（我们假设then为保留关键字）：

5dc7fe1abeb77f7988847278b8be13f8.png

其他示例状态转换图：

  • 无符号数：

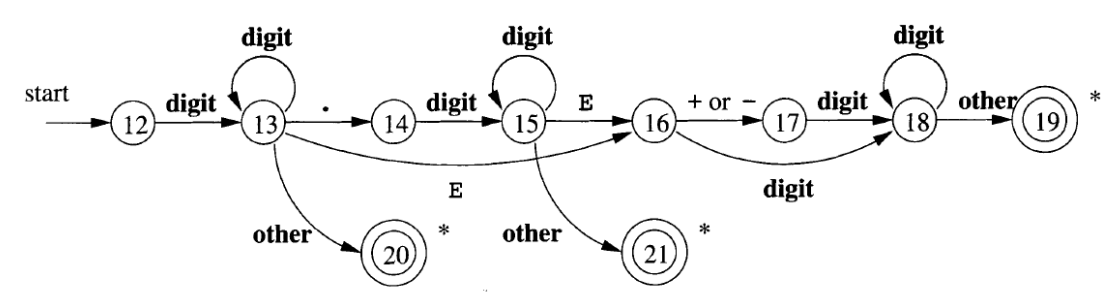
    d864c85e125181e579d2e9e3e2618d12.png

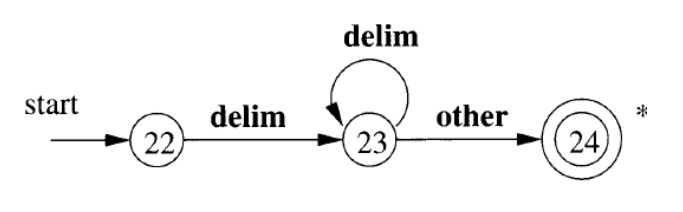
  • 空白符：e08401f536fc422471dd8be839a3b0dd.png

多模式下的识别

词法分析器需要匹配多个模式。

  • 按照优先级，顺序地尝试各个状态转换图，如果引发fail()，回退并尝试下一个状态图。
  • 更好的方法：并行地运行各个状态转换图；通过greedy策略，识别最长的与某个模式匹配的输入前缀。
  • 实际使用的方法：预先把各个状态转换图合成一个状态转换图，然后运行这个状态转换图。

有穷自动机

有穷自动机只回答yes或no。

symbol explanation
Σ 字母表
S 状态集
q0 初始状态
F 终止状态集
δ 转换函数

不确定的有穷自动机（NFA）

所有状态下，对于任意字符（包括ε），有多于一个的状态可以转移。

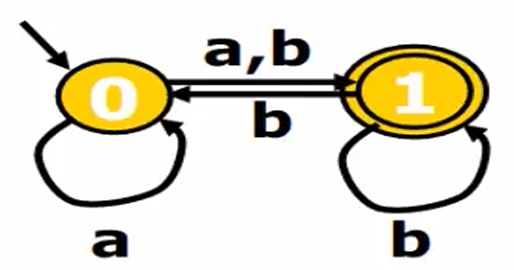
1118cb072b2df07ce9c9ebfc8b41c2ac.png

  • 字母表：
    • { a , b }
  • 状态集：
    • { 0 , 1 }
  • 初始状态：
    • 0

  • 终止状态集：

    • { 1 }

  • 转移函数：

    • {

      ​ (q0 , a) -> { q0 , q1 },

      ​ (q0 , b) -> { q1 },

      ​ (q1 , b) -> { q0 , q1 }

      }

确定的有穷自动机（DFA）

所有状态下，对于任意字符，最多有一个的状态可以转移。

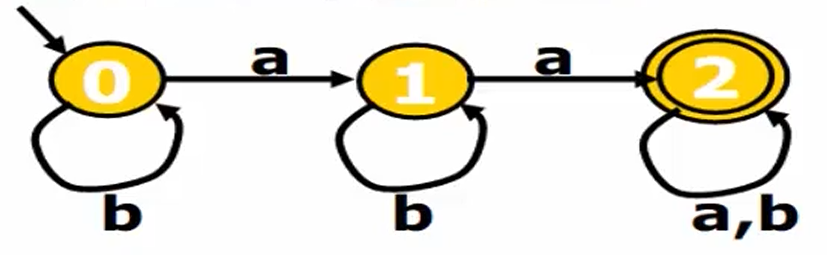
8ce444f53a6b4de930ea2fdf92af1db8.png

  • 字母表：
    • { a , b }
  • 状态集：
    • { 0 , 1 , 2 }
  • 初始状态：
    • 0

  • 终止状态集：

    • { 2 }

  • 转移函数：

    • {

      ​ (q0 , a) -> q1 , (q0 , b) -> q0,

      ​ (q1 , a) -> q2 , (q1 , b) -> q1,

      ​ (q2 , a) -> q2 , (q2 , b) -> q2

      }

regex => NFA（Thompson算法）

根据正则表达式的递归定义，按照正则表达式的结构递归地构造出相应的NFA。

  • ε

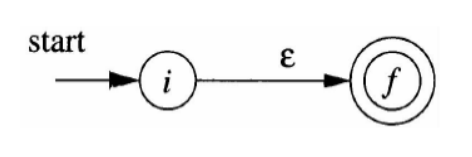
    e91968846234cb33787b43b30b9da8b8.png

  • a

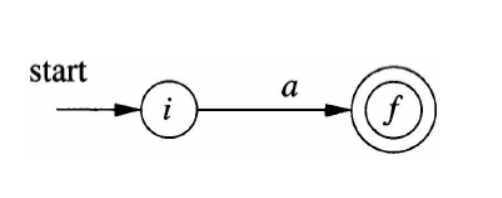
    4d8afffd52b682dd90ecfe29cc9d88ce.png

  • s | t

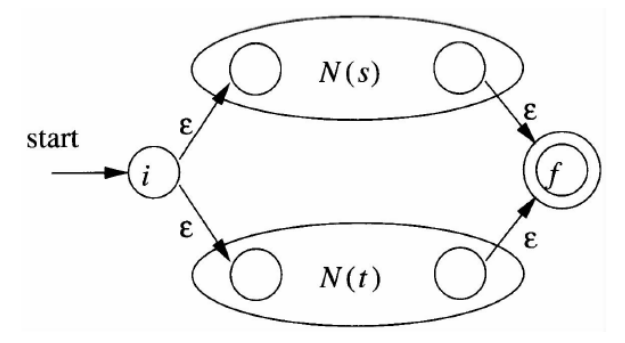
    563372efa5c52b383be5f288fa63368d.png

  • st

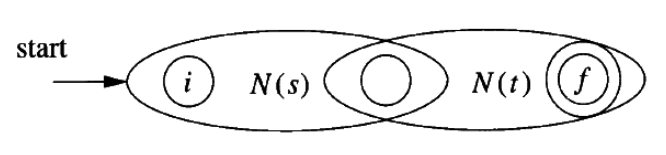
    b856407a2156943f8acf8ce3eb110013.png

  • s*

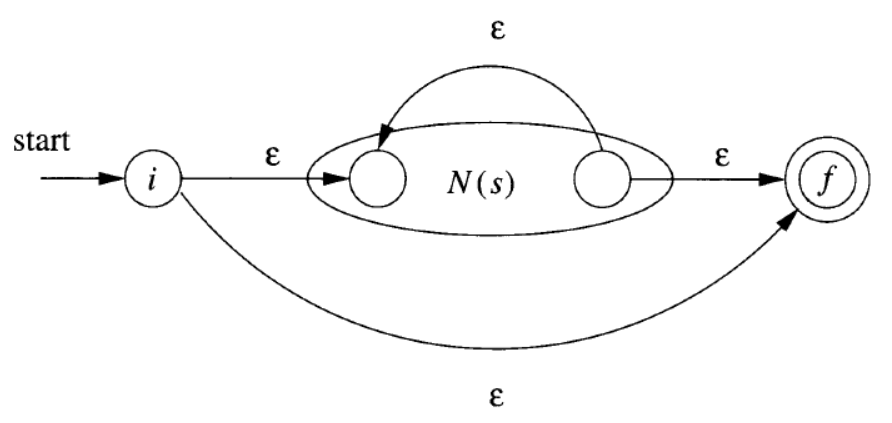
    8249f32a033d9a9d2675e693d213e446.png

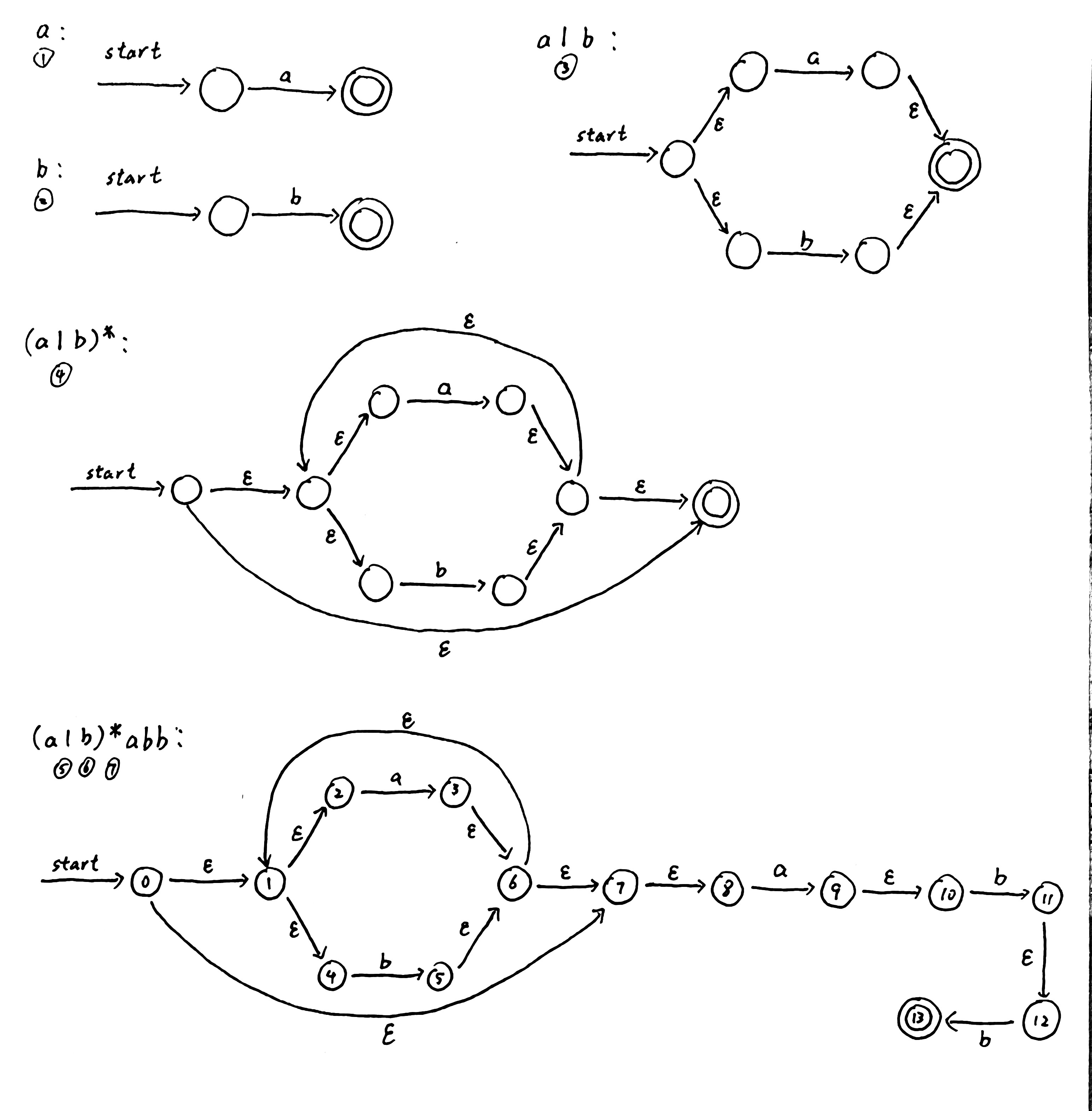
例如我们要描述regex：( a | b )*abb的NFA：

1f678ac408884b74a974904f32e33b87.jpeg

NFA => DFA（子集构造算法）

我们仍借regex：( a | b )*abb的NFA进行研究：

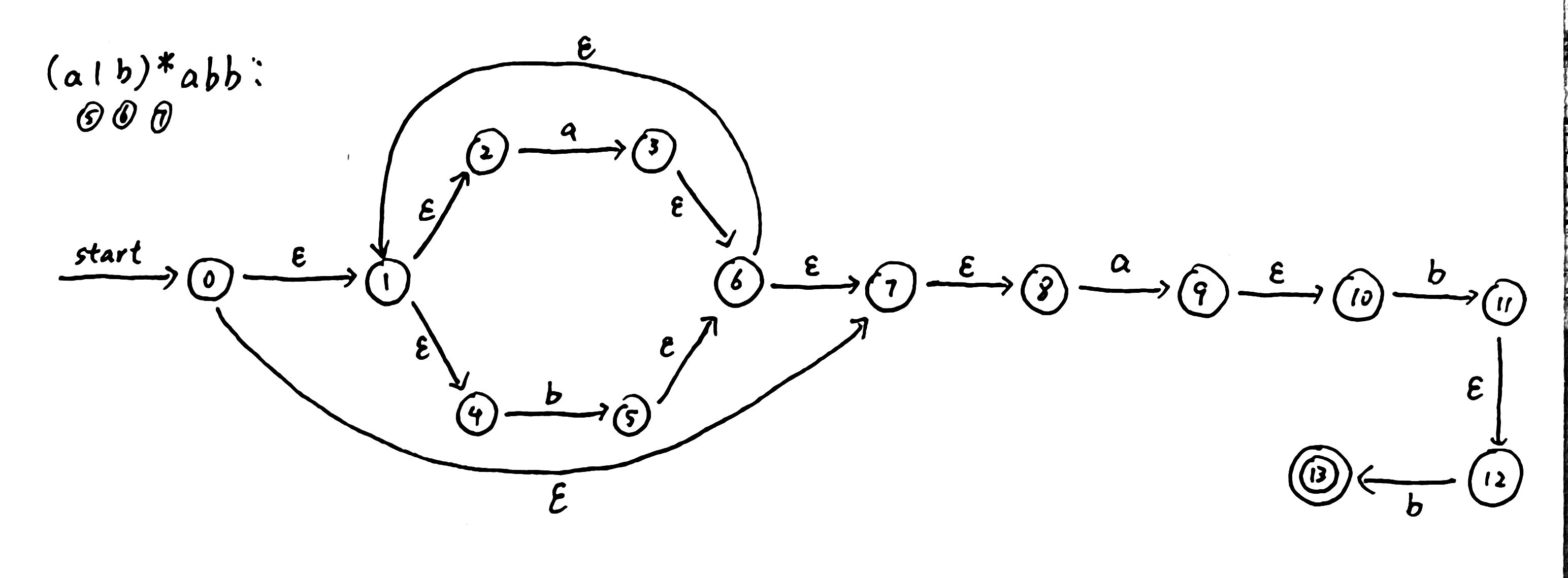
8bc9975647816c3eeafe5aa8e0e4f39d.jpeg

令NFA状态集字母以n，DFA状态集字母以d。

则DFA初始状态为d0。

注意到：

  • n0 =a=> { n1 , n2 , n3 , n6 , n7 , n8 , n4 }
    • 令q1 = { n1 , n2 , n3 , n6 , n7 , n8 , n4 }
    • ∴ q0 =a=> q1
  • q1 =b=> { n2 , n4 , n5 , n6 , n7 , n8 , n4 }

DFA => 词法分析器代码（Hopcroft最小化算法）

语法分析

语法分析器

  1. 从词法分析器获得词法单元的序列，确认该序列是否可以由语言的文法生成。
  2. 对于语法错误的程序，报告错误信息。
  3. 对于语法正确的程序，生成语法分析树 (简称语法树)。

自顶向下语法分析器

通常用于处理LL文法。

从语法分析树的根部开始构造语法分析树。

自顶向下语法分析器

通常用于处理LR文法。

从语法分析树的叶子开始构造语法分析树。

上下文无关文法（CFG）